Op het Wiskunde A eindexamen wordt van je verwacht dat je je algebraïsche vaardigheden op orde hebt. Denk bijvoorbeeld aan breukvormen, wortelvormen, machten en bijzondere producten. Zorg van elk van deze vormen dat je weet hoe je hiermee moet rekenen of een som moet oplossen. Iets complexer is het oplossen van vergelijkingen. Zorg dat je bij vergelijkingen altijd je antwoord controleert door deze opnieuw in de vergelijking te stoppen. Ook moet je eerstegraadsvergelijkingen kunnen oplossen. Zorg dat je de verschillende methoden hiervoor kent en in staat bent snijpunten in grafieken te vinden.
- Leraar: Siska Fitriani
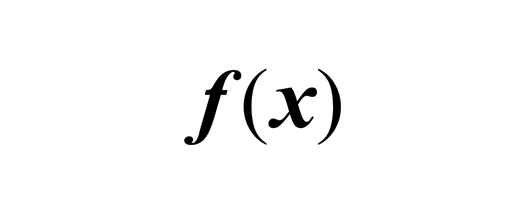
In dit onderdeel komen rekenen en algebra aan de orde. Zorg dat je de voorrangsregels kent bij berekeningen waar haakjes, machten, wortels, vermenigvuldigen, delen, optellen en/of aftrekken terugkomen. Verder wordt van je verwacht dat je met verhoudingen, procenten en afrondingen om kunt gaan. In het onderdeel algebra moet je functies kunnen herleiden door ze simpeler op te schrijven. Daarnaast moet je vergelijkingen op kunnen lossen. Zorg dat je ook alle grootheden kent op het gebied van lengte, oppervlakte, inhoud en gewicht. Je moet in staat zijn om tussen grootheden te rekenen of deze om te zetten naar andere eenheden. Bijvoorbeeld ton naar gram of kubieke meter naar kubieke centimeter. Maar ook bijvoorbeeld liter naar kubieke centimeter.
- Leraar: Siska Fitriani
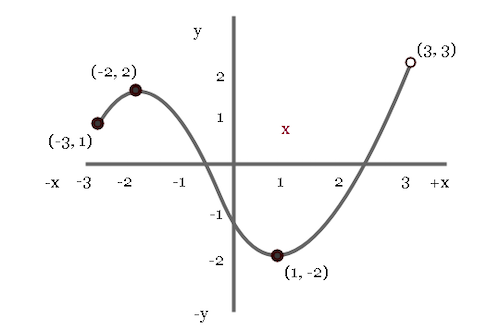
In het onderdeel verbanden moet je weten om te gaan met tabellen en grafieken. Je moet in staat zijn deze af te kunnen lezen en met die informatie verder te rekenen. Zorg dat je bij een grafiek snapt of een lijn stijgt/daalt en of dit toenemend, constant of afnemend is. Ook moet je maxima/minima en snijpunten kunnen opzoeken. Dit laatste moet je onder andere kunnen door vergelijkingen op te lossen en de oplossing van de ene vergelijking in de andere te plaatsen. Ook moet je aan de opbouw van een standaardverband kunnen aflezen hoe de lijn in de grafiek zich beweegt. Is dit bijvoorbeeld lineair, exponentieel, recht evenredig of omgekeerd evenredig? Zorg dat je ook weet hoe de logaritmische schaal werkt.
Om vergelijkingen op te lossen moet je weten hoe je dit kunt doen met behulp van de grafische rekenmachine. Je moet stelsels van vergelijkingen met meerdere onbekenden weten op te lossen. Dit is niet veel moeilijker dan het oplossen van een vergelijking met één onbekende. Je moet hierbij hetzelfde principe alleen een paar keer herhalen. Op het examen moet je zowel met lineaire als exponentiële vergelijkingen kunnen rekenen. Let in alle gevallen op dat het oplossen van een vergelijking nog niet direct het antwoord van de examenvraag geeft. Meestal moet je na het oplossen van de vergelijking verder rekenen met het gevonden antwoord.
- Leraar: Siska Fitriani
Je leert bij een grafiek uitspraken doen over stijgen, dalen, maximum en minimum en kan veranderingen beschrijven met behulp van differenties, hellingen en toenamediagrammen.
- Leraar: Siska Fitriani
Het laatste onderdeel wat op het examen terugkomt is statistiek. Dit onderdeel gaat vooral in op het kunnen verwerken en interpreteren van data. Hiermee kun je vervolgens statistische uitspraken doen. Zorg dat je snapt wat het verschil is tussen een populatie en een steekproef. Steekproeven kunnen op verschillende manieren worden getrokken. Elke vorm heeft voor- en nadelen, welke de uitkomsten van een onderzoek beïnvloeden. Is de steekproef willekeurig gekozen? Weerspiegelt deze de populatie juist? Is de grootte van de steekproef acceptabel voor het onderzoek?
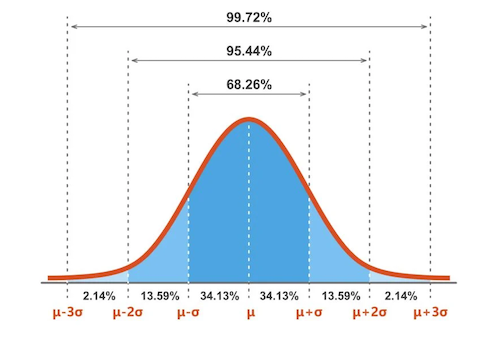
Zorg dat je de verschillen kent tussen het gemiddelde, de modus en de mediaan. Je moet hiermee kunnen rekenen en kunnen aangeven in welke situatie je het best voor wat kunt kiezen. Naast de centrummaten moet je ook de spreidingsmaten kennen. Zorg dat je begrijpt hoe standaardafwijkingen werken. Variabelen kunnen kwalitatief en kwantitatief zijn. Zorg dat je het verschil kent tussen beiden en weet wat discrete en continue variabelen zijn.
Er zijn verschillende tabellen en grafieken die je moet kunnen opstellen en aflezen. Denk hierbij aan de frequentietabel, staafdiagram, dotplot, lijndiagram, cirkeldiagram, steel- en bladdiagram, boxplot, spreidingsdiagram en frequentiepolygoon. Je moet daarnaast weten hoe de normale verdeling werkt en hoe je uitbijters in een grafiek kunt vinden. Uiteindelijk moet je statistische uitspraken kunnen doen en het verschil tussen twee groepen kwantificeren. Zorg dat je hierbij weet wat statistische samenhang en oorzakelijke verbanden zijn.
- Leraar: Siska Fitriani
